Morphing

Overview

This project explored the use of image warping and dissolving to generate hybrid images. The images below are a combination of affine transformations on triangulations, as well as cross-dissolving on those image compartments. This results in beautiful hybrid images that allow for the creation of interesting Photoshop-like effects.

Corespondence

This section demonstrates how correpsondences were calculated. I wrote a python script that collects dots pairs from both images and constructs a triangulation with the Delaunay Triangulation

Original Namu

Original Anwita

The following images show the result of the triangulation

Namu Triangulation

Anwita Triangulation

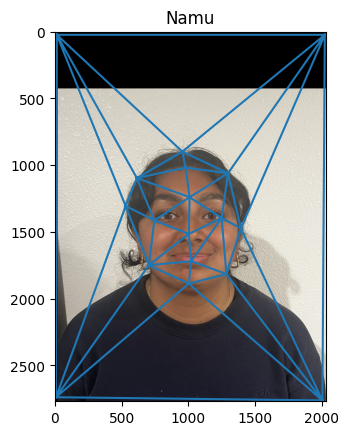
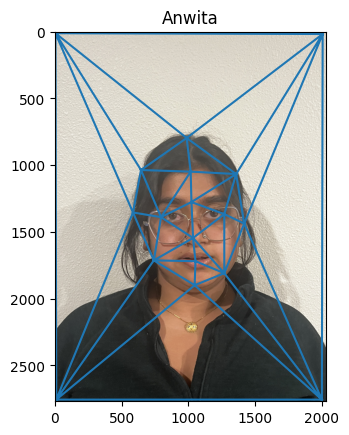
Midway

Using the triangulations from above, I was able to perform a morph and cross-dissolve to create a hybrid image of these two people. The following images show the result. This image was calculated using the following equation: 1/2*(morph(image1) + morph(image2)). The morph function applies an affine transformation from the original triangulation to the average triangulation between both images.

Anwita

Mix of Both

Namu

Morph Sequence

Using the image merging from the previous section, I was able to create sliding morph sequences. Instead of implicitly assuming a 50/50 split, I interpolated the merge of the two images in the morph and cross-dissolve sequence using the following interpolation equation: t*(img1[points/colors] + (1-t)*img2[points/colors]).

Morph Sequence Transition (jitter was used to make it loop)

Mean Face

Using the Brazilian face dataset, I constructed an average face image by averaging the morphed triangulations of the images in the dataset.

Examples of morphed images

Mean Morph 1

Mean Morph 2

Mean Morph 3

Mean Morph 4

Mean Image

Using the transformed images from the previous section, I constructed the average face image by averaging them.

Brazilian Average Face

Caricatures

I also created caricatures of myself by extrapolating my face from the Brazilian average face. This was achieved by adding alpha values above and below 1 and 0 to create some funky images.

Original Image of me

Extrapolation with alpha>1

Extrapolation with alpha<0